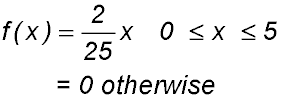Where the techniques of Maths
are explained in simple terms.
Continuous probability density functions.
Test Yourself 1.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
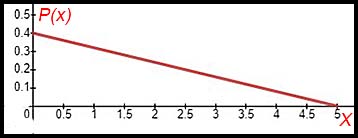
| Properties. | 1. The following diagram shows a probability density function as a line:
Answer. (i) P(x) = 0.4 - 0.08x [0, 5]. The function here is just the usual equation for the line shown. (ii) The area below the line: = 0.5 × 0.4 × 5 = 1.0. Hence a pdf. |
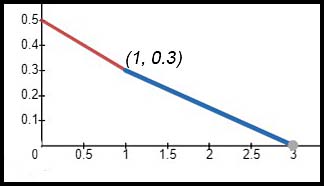
| 2. The following diagram shows a possible probability density function as two lines:
Answer.(i) P(x) = 0.5 - 0.2x [0,1] and P(x) = 0.45 - 0.15x [1, 3]. The function combines the equations for the two lines shown. (ii) Area Trap = 0.4 Area Tri = 0.3 Sum = 0.7. |
|
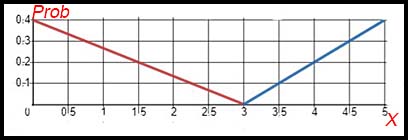
| 3. The following diagram shows a probability density function as two lines:
Answer. P(x) = 0.4 - 0.4x/3 [0,3] and P(x) = 0.2x - 0.6 [3, 5]. The function combines the equations for the two lines shown. |
|
| 4. Show that the function
does not satisfy either of the properties for a probability density function. |
|
5. (i) Show that 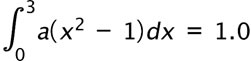 when a = 1/6. when a = 1/6.
(ii) Draw the sketch of y = a( x2 - 1) for that value of a and in the domain [0, 3] showing the x and y intercepts. (iii) Explain why the function y = a(x2 - 1) is not a probability function. |
|
6. A probability density function is defined as 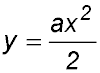 in the domain [0, 3]. in the domain [0, 3].
Find the value of a. Answer. a= 2/9. |
|
7. A function is defined as 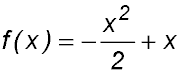
Answer. P(x = 2) = 0.5. |
|
| 8. The probability density function for the random variable x is defined in the domain [0, 2] as
|
|
| Uniformly distributed functions. | 9. David has recently taken up kayaking on a nearby lake to give himself exercise during lockdown. He aims to be on the water for 30 minutes but is presently averaging 24 minutes. The time he spends on the water varies between 18 and 30 minutes.
Answer.(i) Time is continuous and David can stop at any time with equal probability. (ii) P(<20) = 2/6 = 0.33. (iii) P(20 |
10. The International Space Station (ISS) completes an orbit of Earth every 90 minutes (say - the time depends on its height and the time can be up to about 93 minutes). Hence the probability of seeing the Space Station in one minute from now is 1/90 (without checking on the app ISS Live Now). This probability distribution can therefore be regarded as being uniformly distributed.
|
|
| 11. | |
| 12. | |
| 13. | |
| Expected value and variance. | 14. Using the strategy outlined elsewhere, prove that, for a uniform probability distribution function, the variance can be expressed as You can assume that the factorisation of |
| 15. The random variable X has a probability density function defined as:
Find, correct to two decimal places: Answer.(i) P (3.1 ≤ x ≤ 4.5) = 4.3 (ii) E(X) = 3.33. (iii) Var (X) = 1.61. |
|
| 16. | |
| 17. In relation to the uniform distribution for the ISS in Q 7 above, calculate the expected mean time for seeing the ISS pass overhead. | |
| Find the mode. | |
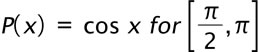
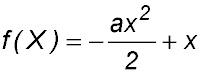 is a probability density function, find the value of a and hence write down the probability density funtion for the domain [0, 2].
is a probability density function, find the value of a and hence write down the probability density funtion for the domain [0, 2]. .
.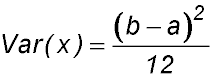 .
.